Modeling Formula 1 Fantasy GP points with PyMC

python
pymc
formula1
Author

Kiril Zvezdarov

Published

August 31, 2023

Code 
%matplotlib inline

import json
import os
import warnings
from enum import Enum
from pathlib import Path

warnings.filterwarnings("ignore", category=UserWarning)
warnings.filterwarnings("ignore", category=FutureWarning)

import arviz as az
import numpy as np
import pandas as pd
import preliz as pz
import pymc as pm
import requests
import seaborn as sns
import tqdm
from matplotlib import pyplot as plt
from scipy import stats

sns.set_theme()
sns.set_style(style="darkgrid", rc={"axes.facecolor": ".9", "grid.color": ".8"})
sns.set_palette(palette="deep")
sns_c = sns.color_palette(palette="deep")

plt.rcParams["figure.figsize"] = [10, 7]

az.style.use("arviz-docgrid")
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

Like many others I got into Formula 1 after binging through Drive to Survive. After enduring a nail biting (and ultimately bitterly disappointing) 2021 season, and attending the 2022 Canadian Grand Prix, I organized a small fantasy league for 2023, hosted on Fantasy GP.

Fantasy GP’s rules give each player a set budget to build a team consisting of 3 drivers and 3 constructor. During the season, drivers and constructors are awarded points for position finished during at the race (matching the actual world championship points awarded), as well as for bonuses such as beating their teammate and gaining positions during the race. This effectively brings lower midfied and backmarker drivers into the mix, since they can generate points from performance relative to their rivals.

This notebook will attempt to model individual driver and constructor performance in terms of Fantasy GP points earned, in order to provide a slightly more quantifiable basis for team construction. We focus on the most fundamental question - how many points per race is a given driver/constructor likely to earn. To answer this, we will create and evaluate a simple Bayesian linear model using the probabilistic programming framework PyMC.

Disclaimer

I have a fairly limited knowledge of Bayesian statistics and modeling; this notebook shouldn’t be considered authoritative of prescriptive in any way. It is mostly a collection of notes, reflecting ongoing learning.

1 Data acquisition

We start by acquiring data for the 2023 season. The Ergast API hosts statistics for Formula 1 races from the 1950s to the present day and exposes convenient endpoints for querying both qualifying and grand prix results.

First, we define some convenience functions to query the raw json data:

API = "http://ergast.com/api/f1"
Code 
DATASET_PATH = {"gp": "results", "quali": "qualifying"}


def get_dataset(dataset: str, year: int, limit: int = 10000) -> dict:
    path = DATASET_PATH[dataset]
    url = f"{API}/{year}/{path}.json?limit={limit}"

    response = requests.get(url)
    response.raise_for_status()

    return response.json()


def load_dataset(dataset: str, year: int) -> dict:
    results_path = Path(f".data/{year}_{dataset}_results.json")

    if results_path.exists():
        with results_path.open() as f:
            results = json.loads(f.read())
    else:
        results = get_dataset(dataset, year)

        if not os.path.isdir(".data"):
            os.makedirs(".data")

        with results_path.open("w") as f:
            f.write(json.dumps(results))

    return results
gp_data = load_dataset("gp", 2023)
quali_data = load_dataset("quali", 2023)

Next, we unnest it into a row-wise format and load it as a Pandas dataframe for ease of use:

Code 
def gp_results_to_dataframe(json_data):
    data = {}
    for gp in json_data["MRData"]["RaceTable"]["Races"]:
        for result in gp["Results"]:
            data.setdefault("circuit", []).append(gp["Circuit"]["circuitId"])
            data.setdefault("driver", []).append(result["Driver"]["code"])
            data.setdefault("round", []).append(gp["round"])
            data.setdefault("constructor", []).append(
                result["Constructor"]["constructorId"]
            )

            data.setdefault("grid", []).append(result["grid"])
            data.setdefault("position", []).append(result["position"])
            data.setdefault("points", []).append(result["points"])
            data.setdefault("fastest_lap", []).append(
                result.get("FastestLap", {}).get("rank")
            )
            data.setdefault("status", []).append(result["status"])

    return (
        pd.DataFrame(data)
        .astype(
            {
                "circuit": "category",
                "driver": "category",
                "round": "int",
                "constructor": "category",
                "status": "category",
                "grid": "Int64",
                "position": "Int64",
                "points": "float32",
                "fastest_lap": "Int64",
            }
        )
        .set_index(["circuit", "driver"])
    )


def quali_results_to_dataframe(json_data):
    data = {}
    for quali in json_data["MRData"]["RaceTable"]["Races"]:
        for result in quali["QualifyingResults"]:
            data.setdefault("circuit", []).append(quali["Circuit"]["circuitId"])
            data.setdefault("driver", []).append(result["Driver"]["code"])
            data.setdefault("round", []).append(quali["round"])
            data.setdefault("constructor", []).append(
                result["Constructor"]["constructorId"]
            )

            data.setdefault("qualifying_position", []).append(result["position"])

    return (
        pd.DataFrame(data)
        .astype(
            {
                "circuit": "category",
                "driver": "category",
                "round": "int",
                "constructor": "category",
                "qualifying_position": "Int64",
            }
        )
        .set_index(["circuit", "driver"])
    )
gp_df = gp_results_to_dataframe(gp_data)
gp_df
round constructor grid position points fastest_lap status
circuit driver
bahrain VER 1 red_bull 1 1 25.0 6 Finished
PER 1 red_bull 2 2 18.0 7 Finished
ALO 1 aston_martin 5 3 15.0 5 Finished
SAI 1 ferrari 4 4 12.0 14 Finished
HAM 1 mercedes 7 5 10.0 10 Finished
... ... ... ... ... ... ... ... ...
monza STR 14 aston_martin 20 16 0.0 17 Finished
HUL 14 haas 13 17 0.0 10 +1 Lap
MAG 14 haas 19 18 0.0 15 +1 Lap
OCO 14 alpine 18 19 0.0 19 Steering
TSU 14 alphatauri 11 20 0.0 <NA> Engine

280 rows × 7 columns

quali_df = quali_results_to_dataframe(quali_data)
quali_df
round constructor qualifying_position
circuit driver
bahrain VER 1 red_bull 1
PER 1 red_bull 2
LEC 1 ferrari 3
SAI 1 ferrari 4
ALO 1 aston_martin 5
... ... ... ... ...
monza ZHO 14 alfa 16
GAS 14 alpine 17
OCO 14 alpine 18
MAG 14 haas 19
STR 14 aston_martin 20

280 rows × 3 columns

Finally, we join the grand prix and qualifying dataframes together, forming the base dataset for our analysis; we also rename all entries credited to Liam Lawson (LAW) to Daniel Ricciardio (RIC), as Fantasy GP credits points from the temporary reserve driver to the driver they replace:

data_df = gp_df.join(quali_df[["qualifying_position"]]).rename(
    level="driver", index={"LAW": "RIC"}
)
data_df
round constructor grid position points fastest_lap status qualifying_position
circuit driver
bahrain VER 1 red_bull 1 1 25.0 6 Finished 1
PER 1 red_bull 2 2 18.0 7 Finished 2
ALO 1 aston_martin 5 3 15.0 5 Finished 5
SAI 1 ferrari 4 4 12.0 14 Finished 4
HAM 1 mercedes 7 5 10.0 10 Finished 7
... ... ... ... ... ... ... ... ... ...
monza STR 14 aston_martin 20 16 0.0 17 Finished 20
HUL 14 haas 13 17 0.0 10 +1 Lap 13
MAG 14 haas 19 18 0.0 15 +1 Lap 19
OCO 14 alpine 18 19 0.0 19 Steering 18
TSU 14 alphatauri 11 20 0.0 <NA> Engine 11

280 rows × 8 columns

2 Fantasy points

Fantasy GP points per team/driver are calculated in the following way:

  • drivers earn the points scored during the grand prix, 10pts for taking pole position, 2pts per position gained on Sunday, and 5 points each for beating their teammate during qualifying and the race itself.
  • constructors earn the points scored by each of their drivers during the grand prix, 1pt per position gained per driver, 5 points if both cars finish, 2 if only one car finishes.

To simplify the problem, we completely ignore sprint races (as should everyone).

The race finish status classification has several detailed categories:

data_df["status"].dtype
CategoricalDtype(categories=['+1 Lap', '+2 Laps', 'Accident', 'Brakes', 'Collision',
                  'Collision damage', 'Electrical', 'Engine', 'Finished',
                  'Mechanical', 'Oil leak', 'Overheating', 'Power loss',
                  'Retired', 'Steering', 'Undertray'],
, ordered=False, categories_dtype=object)

Fantasy GP scoring only cares whether a car finished or not, so we define the following set of categories to indiciate a finish:

STATUS_FINISHED = ["Finished", "+1 Lap", "+2 Laps"]

While our dataset has the WDC points scored per driver/constructor already, positions gained and performance vs. teammate need to be added in:

def add_scoring_cols(df: pd.DataFrame) -> pd.DataFrame:
    return df.assign(
        # Grid value of 0 indicates pit lane start; here we set that to 99
        # to simplify the check for who won out in qualifying.
        grid=lambda x: x["grid"].where(x["grid"] != 0, 20)
    ).assign(
        # Positions gained compared to the starting grid position; scoring doesn't
        # care about positions lost, so we set anything below 0 to 0.
        positions_gained=lambda x: np.maximum(x["grid"] - x["position"], 0),
        # Whether the driver won pole position
        has_pole=lambda x: x["qualifying_position"] == 1,
        # Whether the driver beat their teammate in qualifying
        beat_teammate_quali=lambda x: x.groupby(
            # Each group is per race, per constructor, so only 2 rows - one for each driver.
            ["circuit", "constructor"],
            group_keys=False,
        ).apply(
            # Smaller grid pos. = better; the grid position is compared
            # to the reversed grid array in the group (essentially
            # we create a cartesian product of the grid pos.)
            lambda g: g["grid"]
            < g["grid"].iloc[::-1].values
        ),
        # Same as the previous column, but for finishing position in the race.
        beat_teammate_race=lambda x: x.groupby(
            ["circuit", "constructor"], group_keys=False
        ).apply(
            lambda g: (g["position"] < g["position"].iloc[::-1].values)
            & g["status"].isin(STATUS_FINISHED)
        ),
        has_fastest_lap=lambda x: x["fastest_lap"] == 1,
    )


data_df = add_scoring_cols(data_df)

This leaves us with the following dataframe:

Code 
data_df[
    [
        "grid",
        "positions_gained",
        "beat_teammate_quali",
        "beat_teammate_race",
        "has_pole",
        "has_fastest_lap",
    ]
]
grid positions_gained beat_teammate_quali beat_teammate_race has_pole has_fastest_lap
circuit driver
bahrain VER 1 0 True True True False
PER 2 0 False False False False
ALO 5 2 True True False False
SAI 4 0 False True False False
HAM 7 2 False True False False
... ... ... ... ... ... ... ...
monza STR 20 4 False False False False
HUL 13 0 True True False False
MAG 19 1 False False False False
OCO 18 0 False False False False
TSU 11 0 True False False <NA>

280 rows × 6 columns

Finally, we can score the Fantasy GP points; we define the scoring function for the driver to be the sum of:

  • WDC points
  • 10 for gaining pole position
  • 5 for outqualifying their teammate
  • 5 for outracing their teammate
  • 2 per position gained at the end of the race

Note that a driver who did not finish the race on Sunday can still earn points from the qualifying session.

def score_driver(x):
    return pd.Series(
        x["has_pole"] * 10 + x["beat_teammate_quali"] * 5, dtype=float
    ) + pd.Series(
        x["points"] + x["positions_gained"] * 2 + x["beat_teammate_race"] * 5,
        dtype=float,
    ).where(
        x["status"].isin(STATUS_FINISHED), 0
    )

Scoring for the constructors is defined as:

  • WDC points
  • 5 points if both cars finished, 2 if only one did
  • 1 point per position gained at the end of the race per car
def score_constructor(x):
    finished = x["status"].isin(STATUS_FINISHED)
    match finished.sum():
        case 2:
            finish_bonus = 5
        case 1:
            finish_bonus = 2
        case _:
            finish_bonus = 0

    return x["points"].sum() + x[finished]["positions_gained"].sum() + finish_bonus

Just from the rules definition it is clear that drivers have a higher points earnign ceiling but much higher variance, whereas constructors are more consistent but earn fewer points.

Code 
def score_fantasy_points(df: pd.DataFrame) -> pd.DataFrame:
    return df.assign(
        driver_points=score_driver,
        # Constructor points need to be joined back in on the grouping columns, in order to
        # fill in the missing spots with duplicate values - since we have 20 drivers, but 10 constructors,
        # the group has fewer rows and needs to be broadcast per group on the index.
        constructor_points=lambda x: x.join(
            x.groupby(["circuit", "constructor"])
            .apply(score_constructor)
            .rename("constructor_points"),
            on=["circuit", "constructor"],
        )["constructor_points"],
    )

The scored dataframe looks like this:

Code 
data_df = score_fantasy_points(data_df)
data_df[["driver_points", "constructor_points"]]
driver_points constructor_points
circuit driver
bahrain VER 45.0 48.0
PER 18.0 48.0
ALO 29.0 32.0
SAI 17.0 14.0
HAM 19.0 23.0
... ... ... ...
monza STR 8.0 12.0
HUL 10.0 6.0
MAG 2.0 6.0
OCO 0.0 4.0
TSU 5.0 3.0

280 rows × 2 columns

Note

The constructor points are duplicated per race, since we broadcast those across both drivers.

3 Data exploration

Now we visualize the data to get a better idea of its properties. First, some basic box plots for each driver/constructor:

Code 
sns.set_theme(style="ticks")
f, ax = plt.subplots(figsize=(12, 10))
sns.boxplot(
    data=data_df.reset_index(),
    x="driver_points",
    y="driver",
    palette="pastel",
    whis=[0, 100],
)

sns.stripplot(
    x="driver_points",
    y="driver",
    data=data_df.reset_index(),
    hue="circuit",
    linewidth=0,
    size=5,
    dodge=True,
    palette="muted",
)

ax.xaxis.grid(True)
ax.set(xlabel="points")
ax.set_title("Driver Fantasy GP points 2023");
Figure 1: Fantasy points earned by each driver in 2023

For convenience, we create a constructor-specific dataframe by taking the first row for each constructor for each race. This gets rid of the duplicate data (as constructor points were duplicated across both drivers):

const_data_df = data_df.groupby(["circuit", "constructor"]).first().reset_index()
Code 
sns.set_theme(style="ticks")
f, ax = plt.subplots(figsize=(12, 6))
sns.boxplot(
    data=const_data_df.reset_index(),
    x="constructor_points",
    y="constructor",
    palette="pastel",
    whis=[0, 100],
)

sns.stripplot(
    x="constructor_points",
    y="constructor",
    data=const_data_df.reset_index(),
    hue="circuit",
    palette="muted",
    linewidth=0,
    size=4,
    dodge=True,
)

ax.xaxis.grid(True)
ax.set(xlabel="points")
ax.set_title("Constructor Fantasy GP points 2023");
Figure 2: Fantasy points earned by each constructor in 2023

These look quite similar and expose the brutal reality of Red Bull’s total dominance over the field. Matching our intuition from the rules definition, drivers appear to earn more and have wider variance in points scored, comapred to teams, with the exception of Max Verstappen and his absurd consistency.

Next, we plot the kernel density estimate of the driver points to gain a better idea of the overall distribution:

Code 
g = sns.displot(
    data_df.reset_index(),
    x="driver_points",
    col="driver",
    kind="kde",
    rug=True,
    col_wrap=3,
    fill=True,
)
g.set_axis_labels("points", "density");
Figure 3: Kernel density estimates for fantasy points earned by each driver in 2023
Code 
g = sns.displot(
    const_data_df.reset_index(),
    x="constructor_points",
    col="constructor",
    col_wrap=5,
    kind="kde",
    height=4,
    rug=True,
    fill=True,
)


g.set_axis_labels("points", "density");
Figure 4: Kernel density estimates for fantasy points earned by each constructor in 2023

The distribution of points is spread and somewhat multi-peaked in both cases; again, constructors appear score in a much more consistent range compared to drivers. The pooled observed points distributions are:

Code 
f, axs = plt.subplots(1, 2, figsize=(12, 5), sharey=True)

sns.kdeplot(data_df.reset_index(), x="driver_points", fill=True, ax=axs[0])
sns.kdeplot(const_data_df.reset_index(), x="constructor_points", fill=True, ax=axs[1])
axs[0].set_title("Overall driver points density 2023")
axs[0].set(xlabel="driver points")

axs[1].set_title("Overall constructor points density 2023")
axs[1].set(xlabel="constructor points")

f.tight_layout();
Figure 5: Grouped kernel density estimates for fantasy points by drivers/constructors in 2023

Given that the point distributions between drivers and constructors appear very similar, we’ll focus on constructing models of the driver points, which we can later fit to the constructor data with minor adjustments.

4 Unpooled model

Our first model will be the simplest possible - we just directly estimate the mean points for each driver individually (an intercept-only, unpooled linear model).

4.1 Picking the likelihood

The points data has several properties that stem from the Fantasy GP ruleset:

  • points are discrete
  • points are strictly bound between 0 and 84 (25 for p1 + 1 for fastest lap + 10 for pole position + 10 for beating teammate + 19 * 2 for maximum possible positions gained)
  • most drivers have a few 0 point finishes, but overall it’s very unlikely for a driver to score 0 points consistently.

Because we are modeling discrete, strictly positive points, one of the count distributions is likely an appropriate choice for the likelihood. The Poisson distribution could be a good choice, but the observations appear overdispersed, as measured by the coefficient of dispersion:

Code 
data_df = data_df.reset_index().astype(
    {
        "circuit": "category",
        "driver": "category",
    }
)

dispersion = (
    data_df.groupby("driver")["driver_points"].var()
    / data_df.groupby("driver")["driver_points"].mean()
)
dispersion
driver
ALB     2.016575
ALO     2.458689
BOT     4.663685
DEV     2.808279
GAS    12.389453
HAM     2.238189
HUL     3.298566
LEC     8.306281
MAG     4.909699
NOR     5.876923
OCO     7.848030
PER     3.748745
PIA     6.062937
RIC     2.466667
RUS     5.968760
SAI     6.063976
SAR     6.434705
STR     5.173077
TSU     2.345168
VER     1.030361
ZHO     7.205955
Name: driver_points, dtype: float64

Given that, we will pick the Negative Binomial as our likelihood, since it handles overdispersion better1.

4.2 Choosing the priors

A Negative Binomial likelihood is defined by two parameters - its mean μ, and a shape parameter α. We’ll need to set priors on both.

The mean is restricted to be positive only. The standard way of defining a negative binomial linear model is to set a Normal prior on the mean and use the exponentiation as the inverse link function to make it positive and usable for parameterizing the likelihood. For the actual prior parameters it would be reasonable to go with a fairly uninformative prior, such as Normal(mu=0, sigma=1); in this case, prior knowledge and the ruleset gives us a hunch that we can reasonably expect most drivers’ mean points per race to be somewhere between 5 (backmarker, occasionally beats their teammate, maybe gains a place) and 30 (top driver & team, consistently getting and winning from pole position).

To come up with parameter values for this, we use the PreliZ library to find a maximum entropy Normal distribution with 90% of its mass between 5 and 30 (we take the natural log of those, given the exponential inverse link):

mu_dist = pz.Normal()
pz.maxent(mu_dist, np.log(5), np.log(30), 0.90);
Figure 6: PDF of the prior chosen for μ

The shape parameter α is also strictly positive. Its effect on the likelihood can be best understood by plotting a Negative Binomial for a few different values, while keeping the mean fixed:

Code 
f, axs = plt.subplots(2, 2, figsize=(12, 6), sharey=True)

pz.NegativeBinomial(alpha=0.5, mu=15).plot_pdf(ax=axs[0, 0], legend=False)
axs[0, 0].set_title(f"Negative Binomial with μ: 15, α: 0.5")

pz.NegativeBinomial(alpha=5, mu=15).plot_pdf(ax=axs[0, 1], legend=False)
axs[0, 1].set_title(f"Negative Binomial with μ: 15, α: 5")

pz.NegativeBinomial(alpha=50, mu=15).plot_pdf(ax=axs[1, 0], legend=False)
axs[1, 0].set_title(f"Negative Binomial with μ: 15, α: 50")

pz.NegativeBinomial(alpha=500, mu=15).plot_pdf(ax=axs[1, 1], legend=False)
axs[1, 1].set_title(f"Negative Binomial with μ: 15, α: 500");
Figure 7: Negative binomial distributions with a fixed mean at different shape parameters

As α increases, the tails shrink. We don’t want very high values, as that will restrict the tails too much, but very small values result in absurdly long tails. To handle that, we use a Gamma distribution, with mass strongly concentrated between 1 and 20:

alpha_dist = pz.Gamma()
pz.maxent(alpha_dist, 1, 20, .9);
Figure 8: PDF of the prior chosen for α

Finally, we prepare the data for use within the model. We factorize the driver column into labels and an index:

idx, labels = pd.factorize(data_df["driver"], sort=True)

labels is a categorical variable over the driver names:

CategoricalIndex(['ALB', 'ALO', 'BOT', 'DEV', 'GAS', 'HAM', 'HUL', 'LEC',
                  'MAG', 'NOR', 'OCO', 'PER', 'PIA', 'RIC', 'RUS', 'SAI',
                  'SAR', 'STR', 'TSU', 'VER', 'ZHO'],
                 categories=['ALB', 'ALO', 'BOT', 'DEV', ..., 'STR', 'TSU', 'VER', 'ZHO'], ordered=False, dtype='category')

idx is the flattened (race number, driver) index into the observed race result rows:

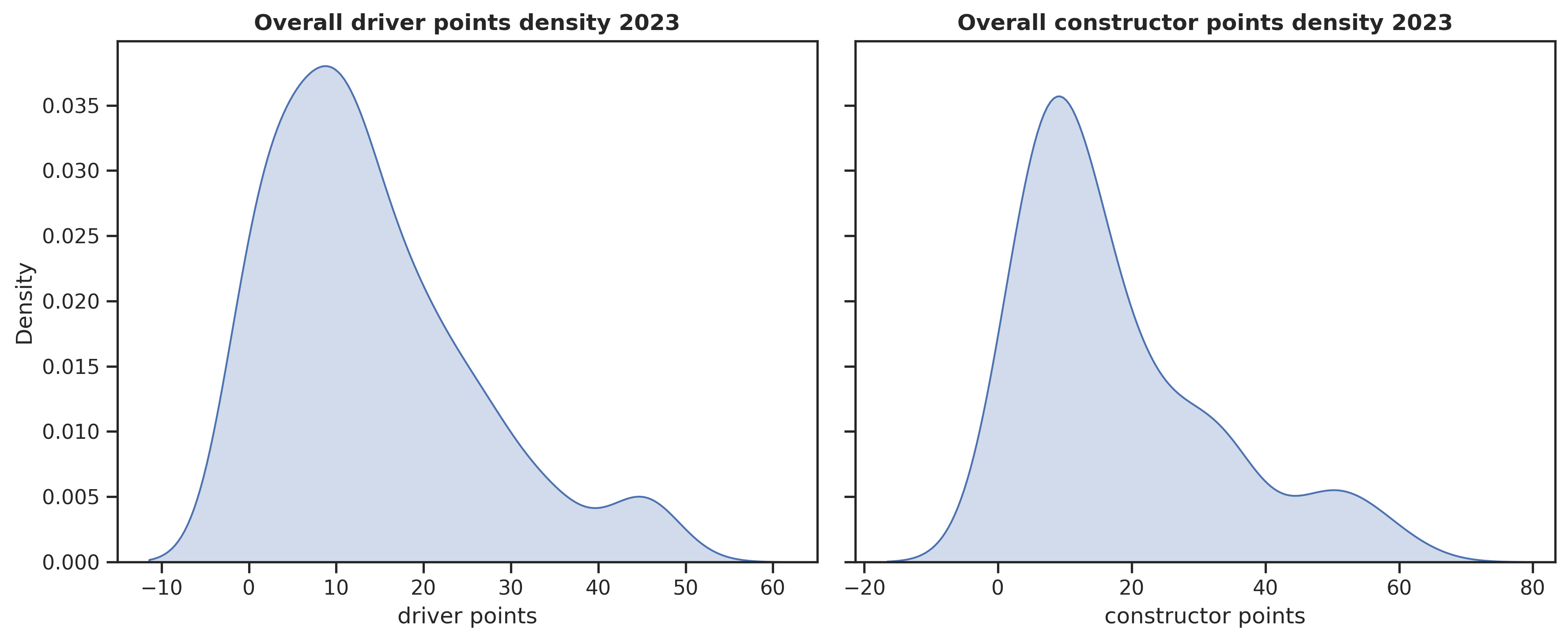
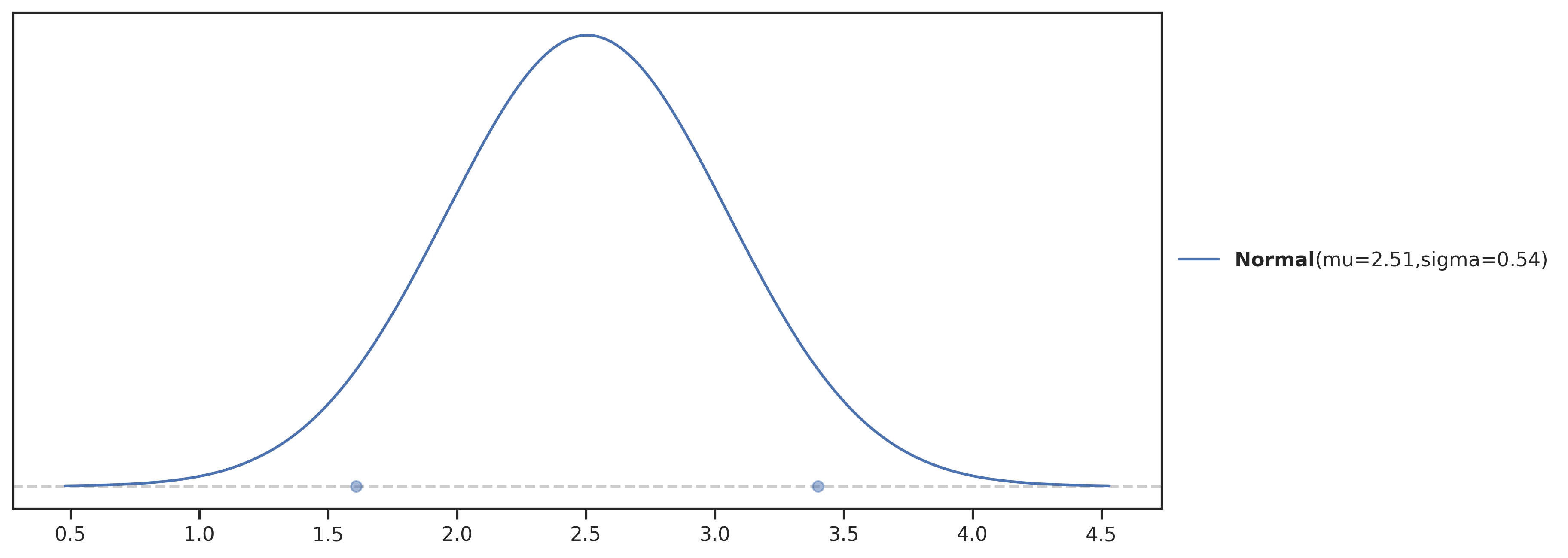
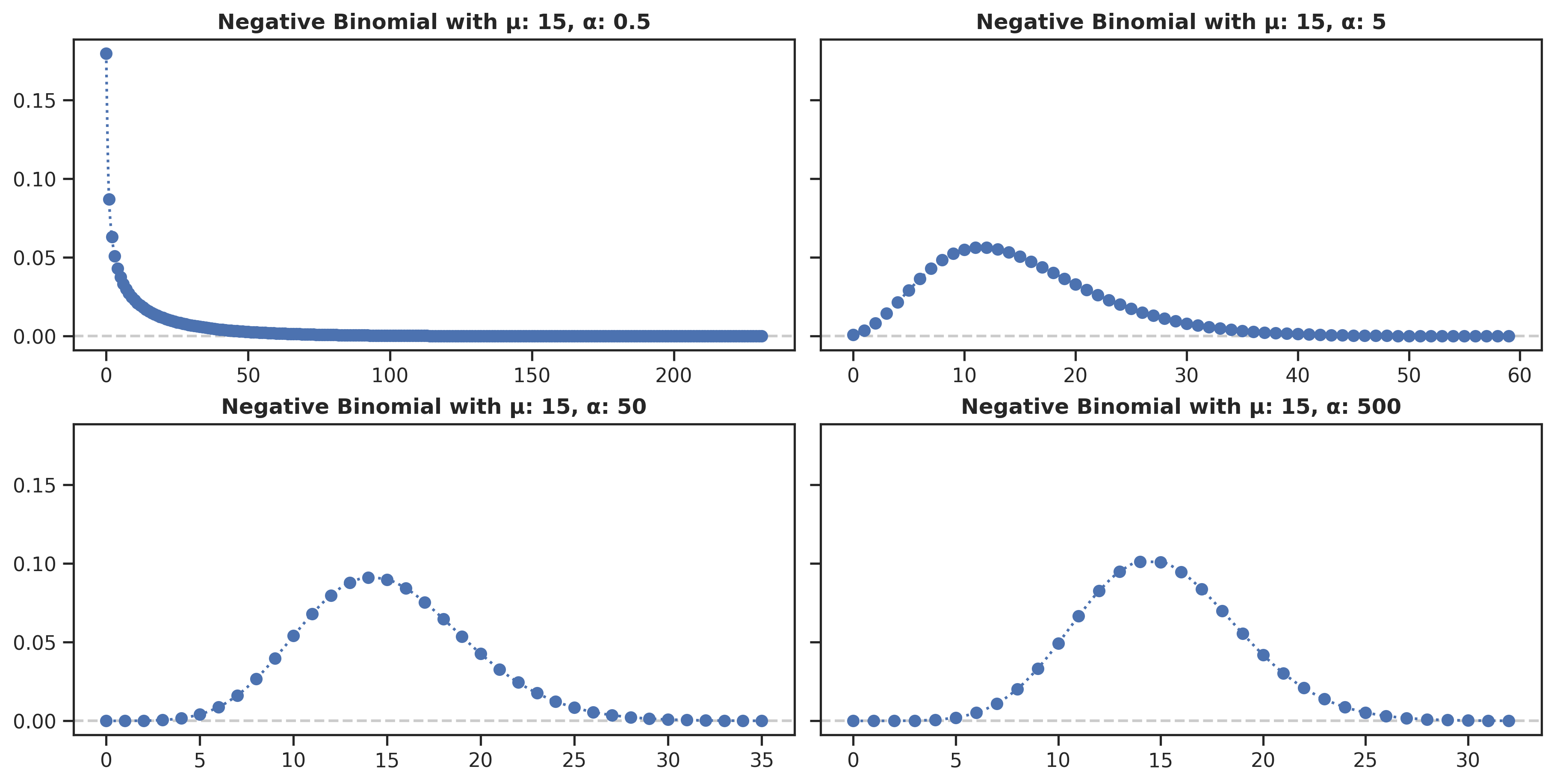
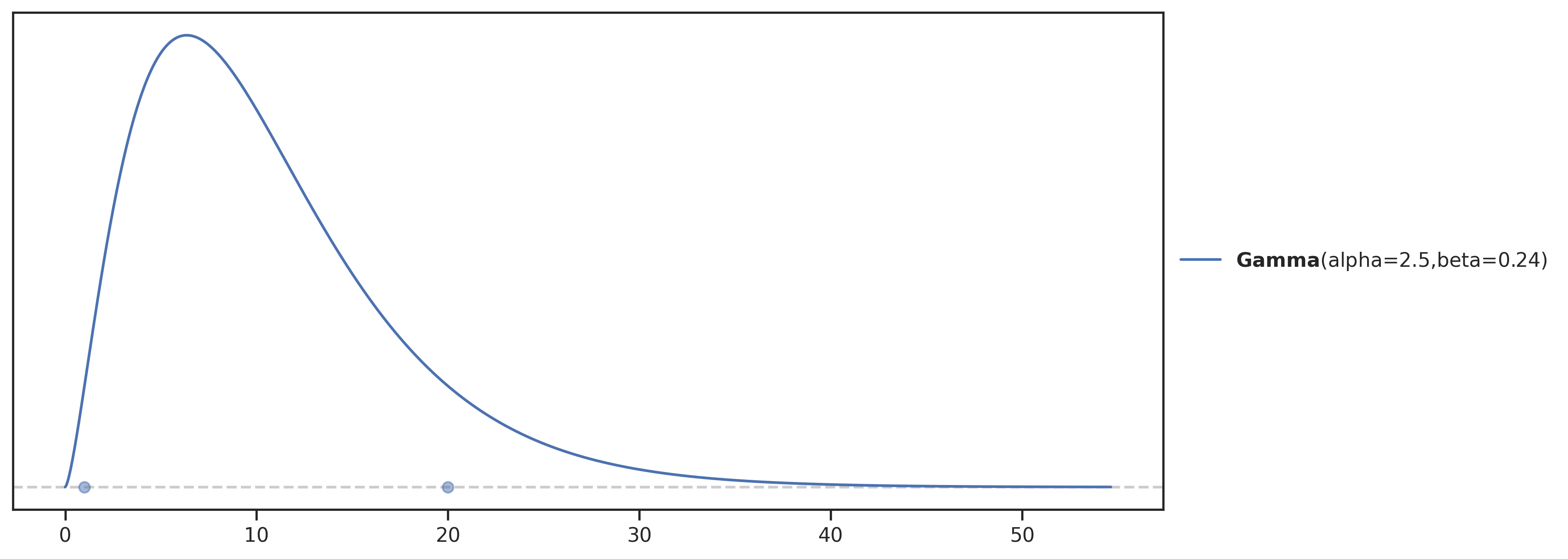
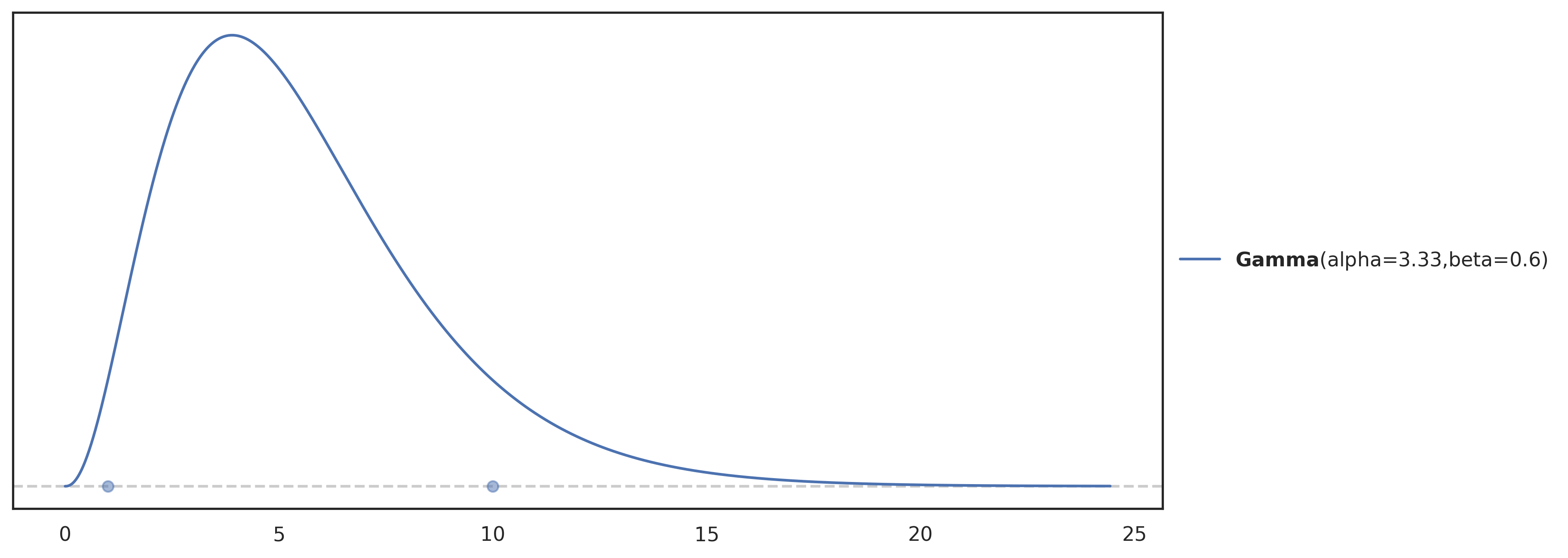
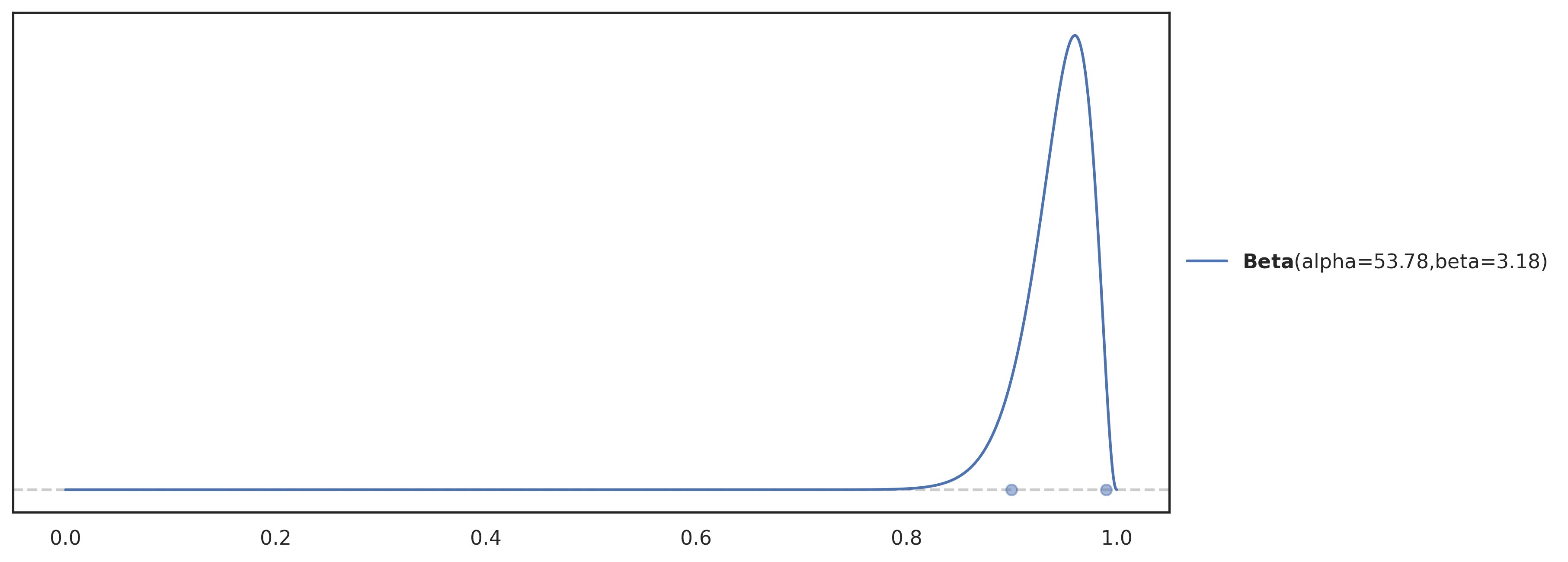
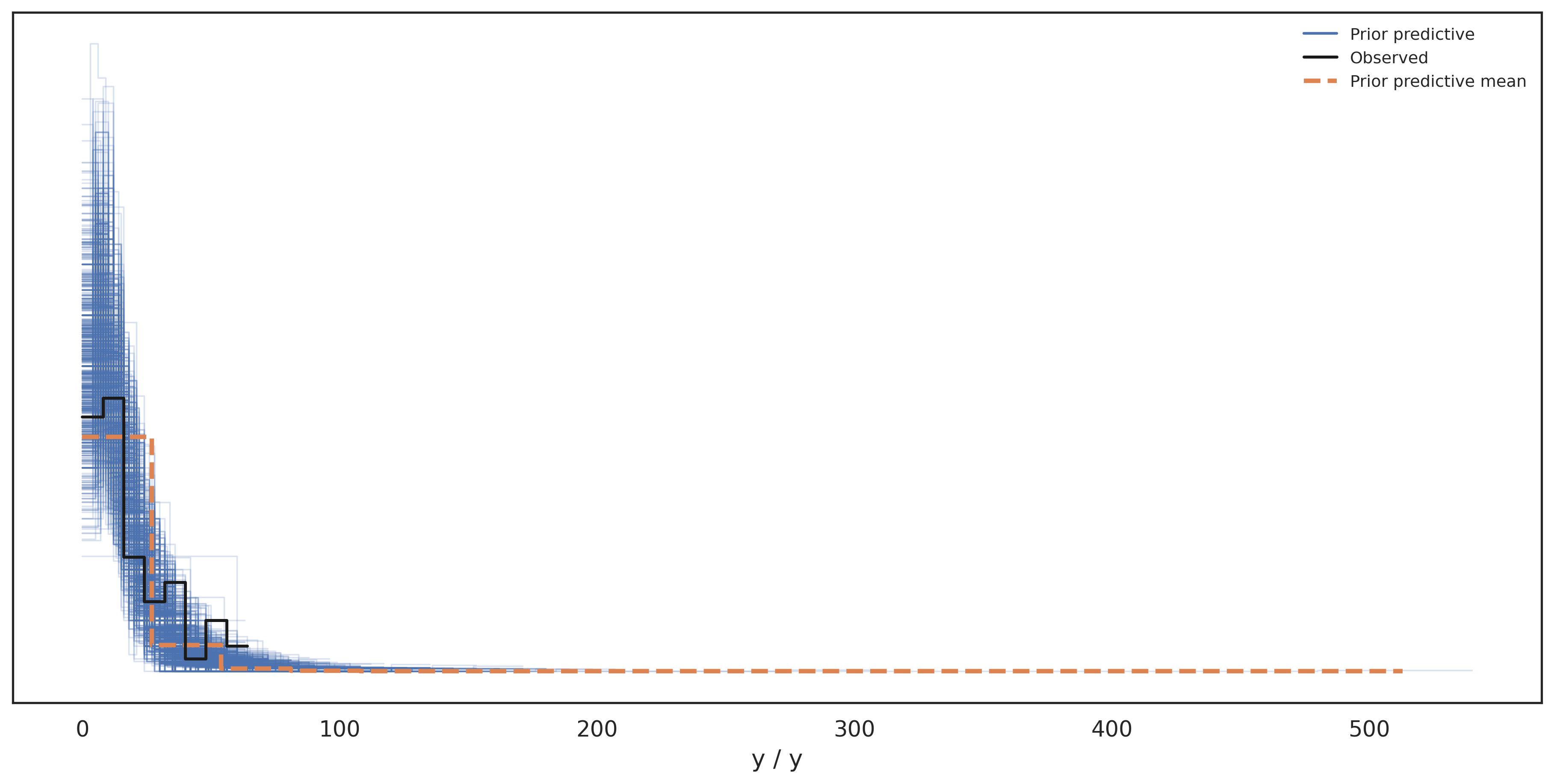
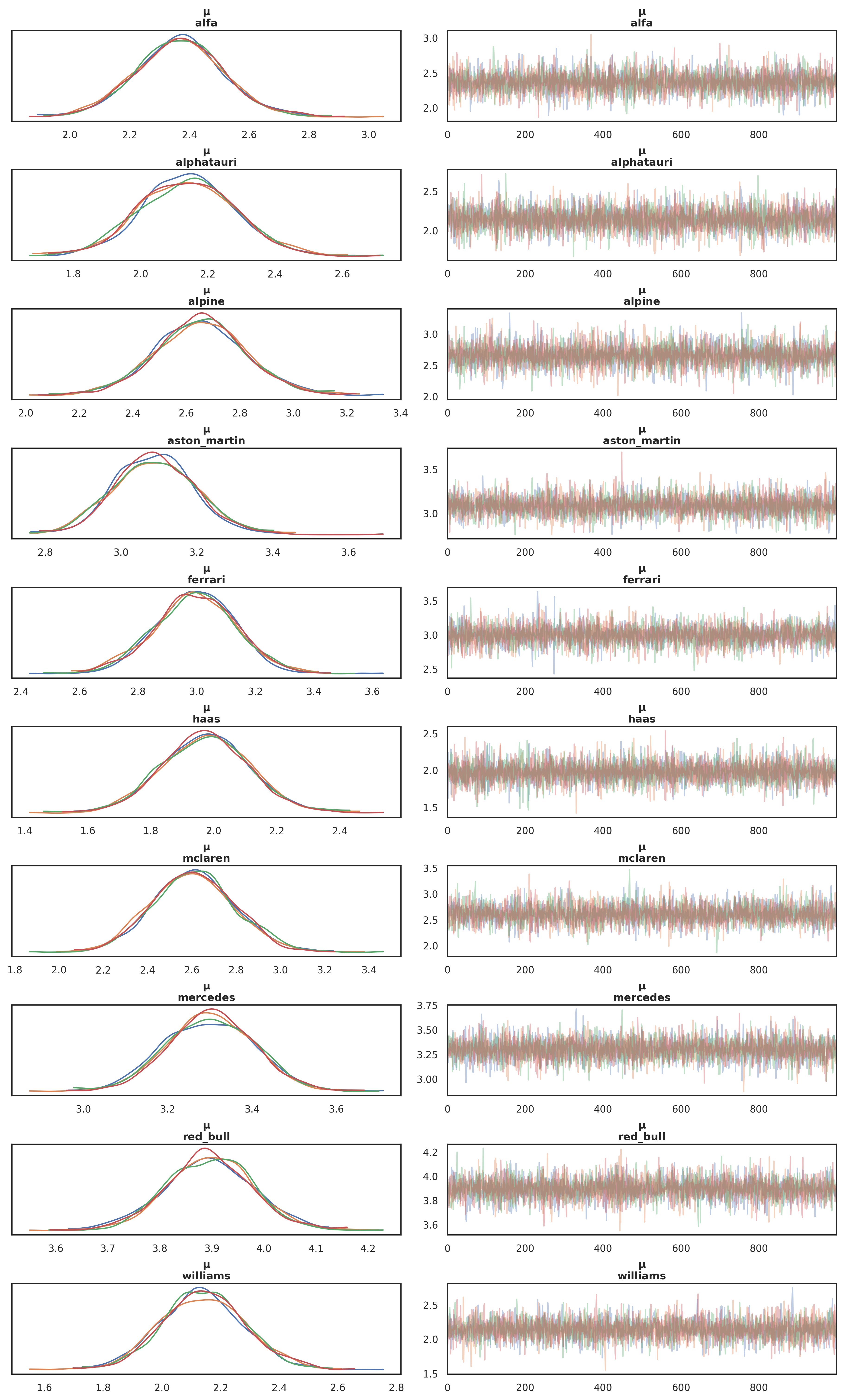
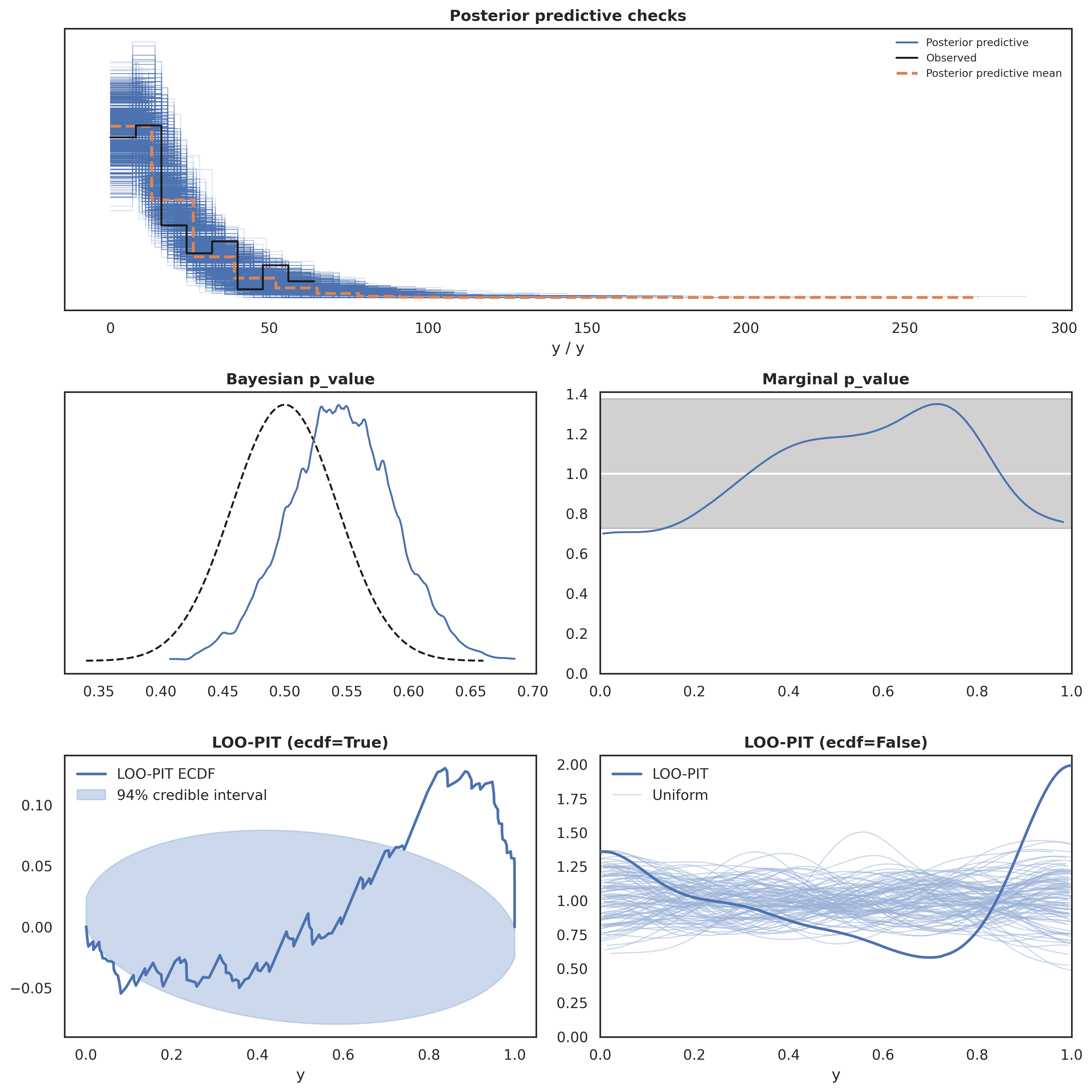
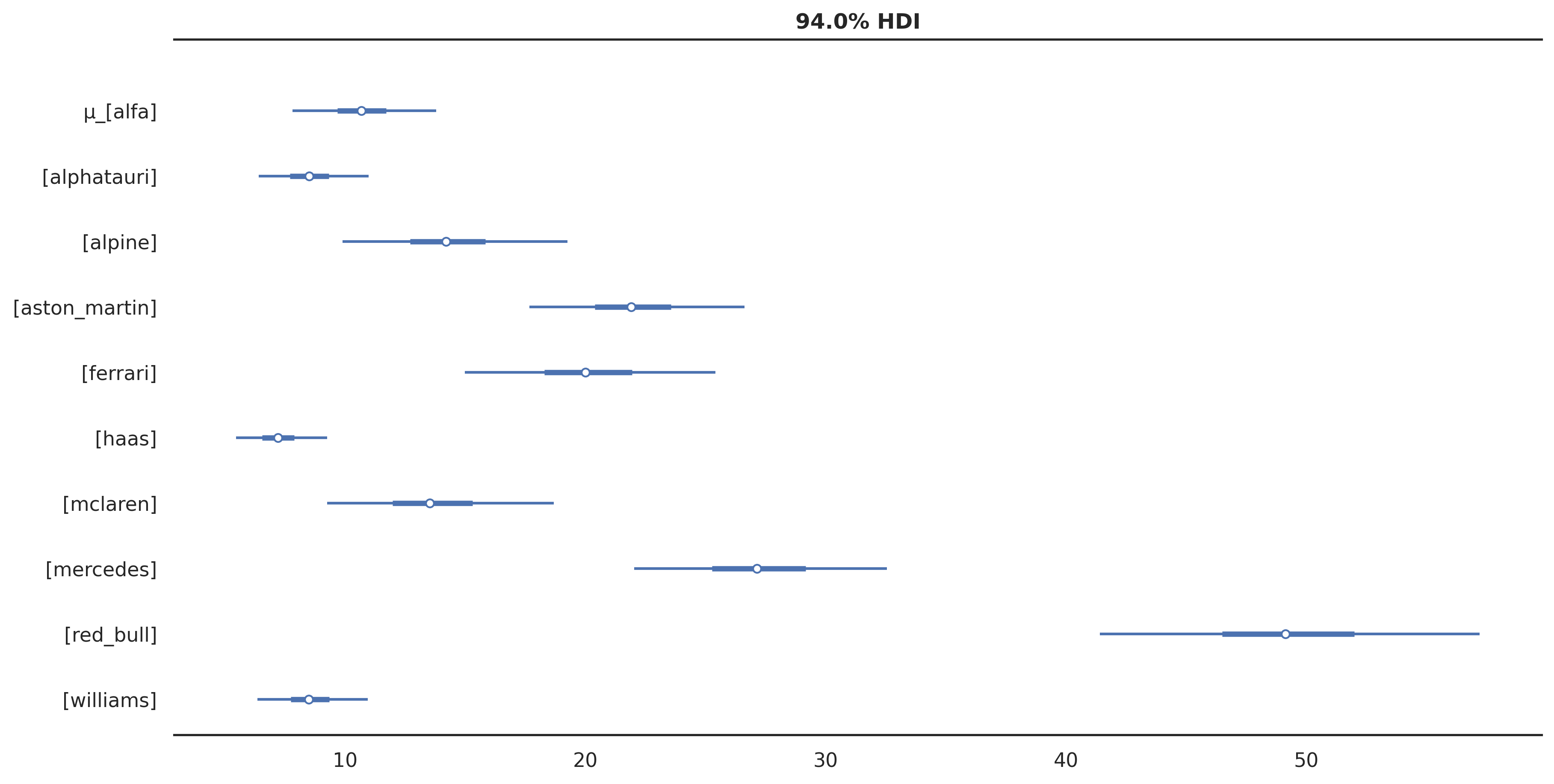
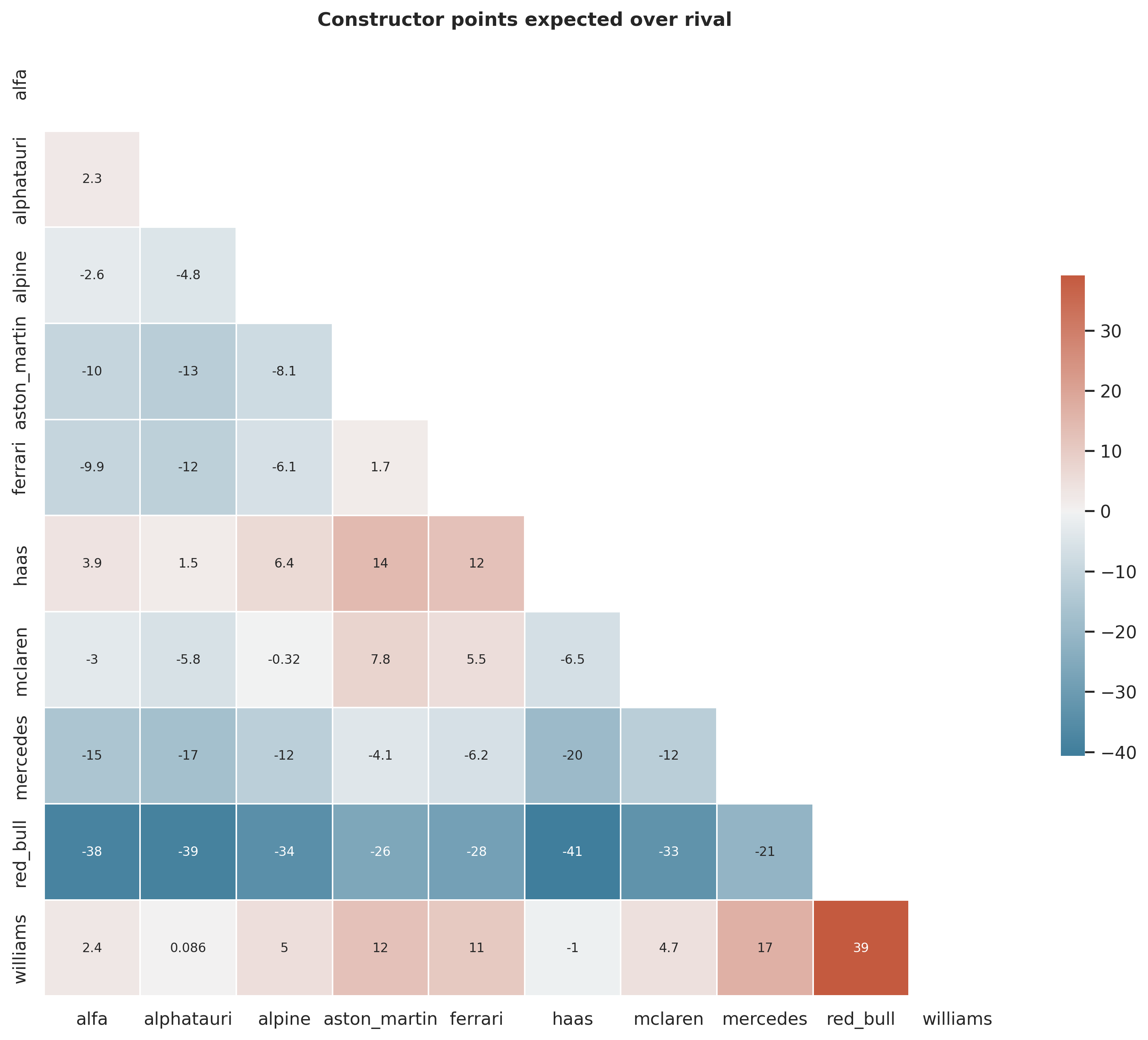
array([19, 11,  1, 15,  5, 17, 14,  2,  4,  0, 18, 16,  8,  3,  6, 20,  9,
       10,  7, 12, 11, 19,  1, 14,  5, 15,  7, 10,  4,  8, 18,  6, 20,  3,
       12, 16,  9,  2,  0, 17, 19,  5,  1, 17, 11,  9,  6, 12, 20, 18,  2,
       15,  4, 10,  3, 16,  8, 14,  0,  7, 11, 19,  7,  1, 15,  5, 17, 14,
        9, 18, 12,  0,  8,  4, 10, 16,  6,  2, 20,  3, 19, 11,  1, 14, 15,
        5,  7,  4, 10,  8, 18, 17,  2,  0,  6, 20,  9,  3, 12, 16, 19,  1,
       10,  5, 14,  7,  4, 15,  9, 12,  2,  3, 20,  0, 18, 11,  6, 16,  8,
       17, 19,  5, 14, 11, 15, 17,  1, 10, 20,  4,  7, 18, 12,  3,  6,  0,
        9,  8,  2, 16, 19,  1,  5,  7, 15, 11,  0, 10, 17,  2, 12,  4,  9,
       18,  6, 20,  8,  3, 14, 16, 19,  7, 11,  9,  1, 15, 14,  5, 17,  4,
        0, 20, 16, 10,  2, 12,  3,  8, 18,  6, 19,  9,  5, 12, 14, 11,  1,
        0,  7, 15, 16,  2,  6, 17, 20, 18,  3,  4,  8, 10, 19,  9, 11,  5,
       12, 14,  7, 15,  1, 17,  0,  2, 13,  6, 18, 20,  8, 16, 10,  4, 19,
       11,  7,  5,  1, 14,  9, 10, 17, 18,  4,  2, 20,  0,  8, 13, 16,  6,
       15, 12, 19,  1,  4, 11, 15,  5,  9,  0, 12, 10, 17,  6, 13,  2, 18,
        8, 14, 20,  7, 16, 19, 11, 15,  7, 14,  5,  0,  9,  1,  2, 13, 12,
       16, 20,  4, 17,  6,  8, 10, 18])

We also extract the observed points:

driver_points = data_df["driver_points"]
driver_points
0      45.0
1      18.0
2      29.0
3      17.0
4      19.0
       ... 
275     8.0
276    10.0
277     2.0
278     0.0
279     5.0
Name: driver_points, Length: 280, dtype: float64

4.3 Model definition

Next, we define the model with PyMC. As discussed previously, we think that the process that generates points can be seen as a Negative Binomial distribution, so that is set as the likelihood. The mean (μ) аnd shape (α) are the parameters that we want to infer from the data. Finally, the prior guesses for these parameters are set from the mu_dist and alpha_dist objects we computed previously.

This translates to:

with pm.Model(coords={"driver": labels, "idx": idx}) as unpooled_negb:
    μ = pm.Normal("μ", mu_dist.mu, mu_dist.sigma, dims="driver")
    μ_ = pm.Deterministic("μ_", pm.math.exp(μ), dims="driver")

    α = pm.Gamma("α", alpha_dist.alpha, alpha_dist.beta, dims="driver")

    y = pm.NegativeBinomial(
        "y", alpha=α[idx], mu=μ_[idx], observed=driver_points, dims="idx"
    )

4.4 Prior predictive checks

To see if the choice for priors is acceptable, we sample from the prior predictive and plot the results:

with unpooled_negb:
    unpooled_prior_samples = pm.sample_prior_predictive(samples=1000)
Sampling: [y, α, μ]
az.plot_ppc(unpooled_prior_samples, group="prior", figsize=(12, 6));
Figure 9: Prior predictive distribution of the unpooled model

The prior predictive is quite wide, with a very long and somewhat fat tail, but overall the data could be plausibly seen as coming from it.

4.5 Inference and diagnostics

Next, we perform the actual inference step - we sample from the posterior and the posterior predictive distribution:

with unpooled_negb:
    unpooled_idata = pm.sample(target_accept=0.9, idata_kwargs={"log_likelihood": True})
    pm.sample_posterior_predictive(unpooled_idata, extend_inferencedata=True)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [μ, α]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 5 seconds.
Sampling: [y]
100.00% [8000/8000 00:04<00:00 Sampling 4 chains, 0 divergences]
100.00% [4000/4000 00:00<00:00]

There are no divergences detected, which is a good first sign that the model has converged.

To check the sampling process we plot the traces for the μ parameter. What we are looking for is similar densities on the left (indicating that the chains have converged to the same posterior distribution), and noisy/patternless trace plots on the right (which would indicate that the sampler was able to efficiently run through the sample space)2:

az.plot_trace(unpooled_idata, var_names=["μ"], compact=False);
Figure 10: Traceplots of the inferred parameter μ for the unpooled model

There are a few kinks here and there (see RIC), but overall these look good.

Next we plot the energy plot and BFMI. Ideally the marginal energy and energy transition distributions should overlap as much as possible, and BFMI should be to be above .3:

Code 
ax = az.plot_energy(unpooled_idata)
ax.set_title("Energy Plot");
Figure 11: Energy plot for the unpooled model

Finally, we check the summary statistics for the μ parameter:

  • bulk and tail effective sample size (ess_bulk and ess_tail respectively) should be > 400, otherwise the estimation of the rest of the summary statistics is considered unreliable 3
  • r_hat should ideally equal 1, with values over 1.01 convergence issues 4
  • mcse_{mean, sd} is the Monte Carlo Standard Error, or the error introduced by approximating the posterior with a finite number of samples; lower = better 5
az.summary(unpooled_idata, var_names=["μ"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
μ[ALB] 2.559 0.113 2.356 2.786 0.002 0.001 5027.0 2717.0 1.0
μ[ALO] 3.124 0.101 2.925 3.308 0.002 0.001 4219.0 2969.0 1.0
μ[BOT] 2.523 0.190 2.158 2.878 0.003 0.002 4131.0 2642.0 1.0
μ[DEV] 1.766 0.220 1.350 2.179 0.004 0.003 3568.0 2298.0 1.0
μ[GAS] 2.459 0.221 2.039 2.874 0.003 0.002 4298.0 2631.0 1.0
μ[HAM] 3.085 0.099 2.907 3.279 0.001 0.001 4774.0 2917.0 1.0
μ[HUL] 2.159 0.151 1.888 2.452 0.002 0.002 4008.0 2570.0 1.0
μ[LEC] 2.723 0.209 2.311 3.114 0.003 0.002 4991.0 2884.0 1.0
μ[MAG] 2.030 0.258 1.552 2.523 0.004 0.003 4224.0 2823.0 1.0
μ[NOR] 2.695 0.146 2.416 2.960 0.002 0.002 4055.0 2487.0 1.0
μ[OCO] 2.275 0.280 1.764 2.818 0.004 0.003 4511.0 2902.0 1.0
μ[PER] 3.283 0.101 3.086 3.472 0.001 0.001 4856.0 3012.0 1.0
μ[PIA] 1.901 0.276 1.373 2.416 0.005 0.003 3901.0 2514.0 1.0
μ[RIC] 2.338 0.226 1.948 2.791 0.003 0.002 4746.0 2388.0 1.0
μ[RUS] 2.776 0.165 2.480 3.097 0.002 0.002 4741.0 2662.0 1.0
μ[SAI] 2.661 0.176 2.338 3.005 0.003 0.002 4280.0 2802.0 1.0
μ[SAR] 1.835 0.451 1.023 2.665 0.007 0.005 4104.0 2613.0 1.0
μ[STR] 2.182 0.260 1.709 2.681 0.004 0.003 3834.0 2291.0 1.0
μ[TSU] 2.420 0.122 2.196 2.660 0.002 0.001 4081.0 2713.0 1.0
μ[VER] 3.742 0.074 3.607 3.886 0.001 0.001 5036.0 2571.0 1.0
μ[ZHO] 2.255 0.237 1.798 2.699 0.003 0.003 4903.0 2624.0 1.0

All of the sampling diagnistics look good, which means the model has converged and we can move on to posterior predictive checks and model evaluation.

4.6 Posterior predictive checks

Next we examine the posterior predictive distribution, which will help validate that the predictions the model is making make sense given the data. Below we plot several posterior graphs (from top to bottom, left to right):

  • the (grouped) posterior predictive distribution should closely replicate the pattern seen in the observed data 6
  • the Bayesian p-value is the probability of the predicted data being equal to or less than the observed data. The ideal/expected outcome is represented by the dashed line (0.5), with the solid line being the KDE of the predicted data; the u-value represents the same idea as the p-value, but per observation - it should be roughly uniform 7
  • LOO-PIT is the probability integral transform checed with LOO-CV; this should be close to uniform; difference between LOO-PIT empirical cumulative distribution function and the uniform cdf 8
Code 
def plot_posterior_predictive_checks(idata):
    f = plt.figure(figsize=(12, 12))

    ax_ppc = f.add_subplot(3, 1, 1)
    az.plot_ppc(idata, ax=ax_ppc)
    ax_ppc.set_title("Posterior predictive checks")

    ax_bpv = f.add_subplot(3, 2, 3)
    az.plot_bpv(idata, kind="p_value", ax=ax_bpv)
    ax_bpv.set_title("Bayesian p_value")

    ax_uv = f.add_subplot(3, 2, 4)
    az.plot_bpv(idata, kind="u_value", ax=ax_uv)
    ax_uv.set_title("Marginal p_value")

    ax_loo_pit_ecdf = f.add_subplot(3, 2, 5)
    az.plot_loo_pit(idata, y="y", ecdf=True, ax=ax_loo_pit_ecdf)
    ax_loo_pit_ecdf.set_title("LOO-PIT (ecdf=True)")

    ax_loo_pit = f.add_subplot(3, 2, 6)
    az.plot_loo_pit(idata, y="y", ecdf=False, ax=ax_loo_pit)
    ax_loo_pit.set_title("LOO-PIT (ecdf=False)")

    f.tight_layout()

    return (ax_ppc, ax_bpv, ax_uv, ax_loo_pit_ecdf, ax_loo_pit)
plot_posterior_predictive_checks(unpooled_idata);
Figure 12: Posterior predictive checks, u/p-value, and LOO for the unpooled model

From the posterior predictive plots it seems that:

  • the posterior predictive samples roughly look like tha observed data, but the fit around the right tail isn’t the best.
  • the p-value plot shows that the model’s predictions are somewhat shifted to the right and the u-value plot indicates that the model is missing observations in the left tail 9
  • LOO-PIT shows the model is likely biased, which agrees with the p/u-value plots.

Lastly, let’s plot the posterior predictive distributions for a few individual drivers:

Code 
fig, axs = plt.subplots(2, 2, figsize=(12, 6))

DriverIdx = Enum("Driver", zip(labels.categories, labels.codes))

az.plot_ppc(unpooled_idata, coords={"idx": [DriverIdx.VER.value]}, ax=axs[0, 0])
axs[0, 0].set_title("VER")

az.plot_ppc(unpooled_idata, coords={"idx": [DriverIdx.SAR.value]}, ax=axs[0, 1])
axs[0, 1].set_title("SAR")

az.plot_ppc(unpooled_idata, coords={"idx": [DriverIdx.LEC.value]}, ax=axs[1, 0])
axs[1, 0].set_title("LEC")

az.plot_ppc(unpooled_idata, coords={"idx": [DriverIdx.HAM.value]}, ax=axs[1, 1])
axs[1, 1].set_title("HAM");
Figure 13: Posterior predictive plots of individual drivers for the unpooled model

4.7 Posterior evaluation

We are reasonably confident that the model has converged and that there were no issues during sampling. Predictions seem to be somewhat biased, but still reasonable for our purposes. Now it’s time to check the posterior distributions of the estimated parameter μ:

az.plot_posterior(unpooled_idata, var_names=["μ"]);
Figure 14: Posterior distributions of the μ parameter for the unpooled model

The estimates look well formed; to make comparing the parameter value between drivers easier, we plot a forest of the 94% HDI 10:

az.plot_forest(unpooled_idata, var_names=["μ"], combined=True, figsize=(12, 6));
Figure 15: Forest of the posterior distributions of μ for the unpooled model (log scale)

The probability distributions for the means broadly agree with our informal observations throughout the season - VER is scoring high above the rest, in an extremely consistent range, with HAM, ALO, and PER close to eachother for second place, a mixed, variable set of results for the midfield, and a few clear backmarker drivers.

To translate the estimated parameter values to points, we can plot the transformed μ_ value (remember that this is just the exponentiated μ):

az.plot_forest(unpooled_idata, var_names=["μ_"], combined=True, figsize=(12, 6));
Figure 16: Forest of the posterior distributions of μ for the unpooled model

4.8 Model evaluation

Finally, we inspect PSIS-LOO-CV to get an idea of the performance of the model:

az.loo(unpooled_idata)
Computed from 4000 posterior samples and 280 observations log-likelihood matrix.

         Estimate       SE
elpd_loo  -954.78    14.99
p_loo       44.52        -

There has been a warning during the calculation. Please check the results.
------

Pareto k diagnostic values:
                         Count   Pct.
(-Inf, 0.5]   (good)      274   97.9%
 (0.5, 0.7]   (ok)          5    1.8%
   (0.7, 1]   (bad)         1    0.4%
   (1, Inf)   (very bad)    0    0.0%

elpd_loo 11 will be more useful when comparing this baseline model to other, more complicated ones, but the fact that Pareto k values are all significantly below 0.7 is a good sign that the model can generalize decently.

5 Zero-inflated unpooled model

One of the common issues with both Poisson and Negative Binomial models is that they do not generate zeroes often enough. This can be alleviated by using a mixture model that inflates the number of zeroes, which PyMC already has an implementation of - the Zero Inflated Negative Binomial likelihood.

To test that extra zeroes might result in a better fit, we define a new model with the same priors as before, but using the mixture likelihood. One additional parameter, ψ, is needed, so we have to set a prior over that. ψ is the probability of a non-zero value, between 0 and 1. We will use a Beta as the prior distribution, and given the ruleset and reliability of modern F1 cars, our prior belief is that 0 point finishes aren’t all that likely. To express that, we take the maximum entropy Beta whose mass is concentrated between .8 and .99:

5.1 Choosing priors

psi_dist = pz.Beta()
pz.maxent(psi_dist, 0.7, 0.99, 0.75);
Figure 17: Prior distribution for the ψ parameter (probability of a non-zero value)

5.2 Model definition

The new model is trivial to define:

with pm.Model(coords={"driver": labels, "idx": idx}) as zi_unpooled_negb:
    μ = pm.Normal("μ", mu_dist.mu, mu_dist.sigma, dims="driver")
    μ_ = pm.Deterministic("μ_", pm.math.exp(μ), dims="driver")

    α = pm.Gamma("α", alpha_dist.alpha, alpha_dist.beta, dims="driver")

    ψ = pm.Beta("ψ", psi_dist.alpha, psi_dist.beta, dims="driver")

    y = pm.ZeroInflatedNegativeBinomial(
        "y",
        psi=ψ[idx],
        alpha=α[idx],
        mu=μ_[idx],
        observed=driver_points,
        dims="idx",
    )

5.3 Prior evaluation

We perform the same prior predictive check:

with zi_unpooled_negb:
    zi_unpooled_prior_samples = pm.sample_prior_predictive(samples=1000)
Sampling: [y, α, μ, ψ]
az.plot_ppc(zi_unpooled_prior_samples, group="prior");
Figure 18: Prior predictive distribution for the zero-inflated model

5.4 Inference and diagnostics

Sample:

with zi_unpooled_negb:
    zi_unpooled_idata = pm.sample(
        target_accept=0.9, idata_kwargs={"log_likelihood": True}
    )
    pm.sample_posterior_predictive(zi_unpooled_idata, extend_inferencedata=True)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [μ, α, ψ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 10 seconds.
Sampling: [y]
100.00% [8000/8000 00:09<00:00 Sampling 4 chains, 0 divergences]
100.00% [4000/4000 00:05<00:00]

The traceplots look about as good as before:

az.plot_trace(zi_unpooled_idata, var_names=["μ"], compact=False);
Figure 19: Traceplots of the μ parameter for the zero-inflated model

BFMI and energy are reasonable:

Code 
ax = az.plot_energy(zi_unpooled_idata)
ax.set_title("Energy Plot");
Figure 20: Energy plot for the zero-inflated model

r_hat and ESS look good as well:

az.summary(zi_unpooled_idata, var_names=["μ"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
μ[ALB] 2.558 0.111 2.343 2.762 0.001 0.001 6450.0 3026.0 1.0
μ[ALO] 3.123 0.100 2.942 3.322 0.001 0.001 6609.0 2903.0 1.0
μ[BOT] 2.655 0.128 2.417 2.900 0.002 0.001 6154.0 2859.0 1.0
μ[DEV] 1.907 0.183 1.581 2.273 0.002 0.001 7928.0 2908.0 1.0
μ[GAS] 2.499 0.208 2.115 2.907 0.003 0.002 6758.0 2526.0 1.0
μ[HAM] 3.082 0.097 2.898 3.264 0.001 0.001 7940.0 2852.0 1.0
μ[HUL] 2.222 0.139 1.965 2.484 0.002 0.001 6692.0 2804.0 1.0
μ[LEC] 2.876 0.143 2.590 3.128 0.002 0.001 6002.0 2722.0 1.0
μ[MAG] 2.237 0.149 1.947 2.507 0.002 0.001 6121.0 2629.0 1.0
μ[NOR] 2.700 0.144 2.436 2.974 0.002 0.001 7691.0 3154.0 1.0
μ[OCO] 2.511 0.166 2.197 2.832 0.002 0.002 6137.0 2785.0 1.0
μ[PER] 3.282 0.105 3.080 3.478 0.001 0.001 6747.0 2638.0 1.0
μ[PIA] 2.078 0.183 1.698 2.395 0.002 0.002 5952.0 2692.0 1.0
μ[RIC] 2.335 0.216 1.906 2.717 0.003 0.002 7119.0 2722.0 1.0
μ[RUS] 2.850 0.135 2.612 3.122 0.002 0.001 5916.0 2873.0 1.0
μ[SAI] 2.728 0.154 2.448 3.019 0.002 0.001 5981.0 2686.0 1.0
μ[SAR] 2.036 0.213 1.672 2.461 0.003 0.002 4655.0 2695.0 1.0
μ[STR] 2.420 0.135 2.167 2.681 0.002 0.001 6232.0 2915.0 1.0
μ[TSU] 2.417 0.123 2.177 2.641 0.001 0.001 7217.0 2763.0 1.0
μ[VER] 3.742 0.074 3.609 3.890 0.001 0.001 6489.0 2464.0 1.0
μ[ZHO] 2.424 0.161 2.105 2.713 0.002 0.001 6419.0 2791.0 1.0

5.5 Posterior predictive checks

Posterior predictive checks look somewhat better:

  • the posterior predictive fits about as well, with a slightly thinner tail
  • p-value is still shifted
  • u-value is much closer to uniform
  • LOO-PIT still suggests bias, but it looks slightly better overall; the right tail of the posterior predictive still looks too fat and goes well above the maximum points possible in the ruleset, likely causing the bias and shifted predictions.
plot_posterior_predictive_checks(zi_unpooled_idata);
Figure 21: Posterior predictive checks, p/u-value, and LOO for the zero-inflated model

5.6 Posterior evaluation

We plot just the forest of transformed means:

az.plot_forest(zi_unpooled_idata, var_names=["μ_"], combined=True, figsize=(12, 6));
Figure 22: Forest plot of the posterior distribution of the exponentiated μ parameter for the zero-inflated model

As expected, compared to the basic model, the means have been pulled towards zero slightly and the HDIs have shrunk.

5.7 Model comparison

Now that we have two models it’s worth running a comparison to see which performs better 12:

Code 
comparison = az.compare(
    {"unpooled": unpooled_idata, "zero inflated unpooled": zi_unpooled_idata}
)
comparison
rank elpd_loo p_loo elpd_diff weight se dse warning scale
zero inflated unpooled 0 -922.394375 40.951957 0.000000 0.787666 17.265214 0.000000 False log
unpooled 1 -954.778337 44.522890 32.383962 0.212334 14.990548 11.918236 True log 
az.plot_compare(comparison);
Figure 23: Comparison of the performance of the unpooled and zero-inflated models

The zero-inflated model clearly seems to perform better 13.

6 Driver estimates

We have a reasonable looking, if a bit biased model for driver points, which we’ll now use to inform fantasy team construction.

When picking drivers, we consider the following:

  • how many points per race is the driver expected to bring and how reliably
  • how likely is it that a given driver will outperform another driver, and by what magnitude
  • how underpriced/overpriced is a a driver given their performance

While price analysis is out of the scope of this notebook, the points estimation model can help us with the first two questions.

Below, we compare each driver to their rivals, using the difference of predicted points per race. To do so, we take the predictions generated from the posterior predictive distribution for each driver, subtract the two vectors, and take the mean. This reduces the posterior distributions to a point estimate, but still incorporates the uncertainty of the model, as we work directly with values generated from the posterior. The value can be seen both as confidence driver x is better than driver y - higher is better, and as the points we expect driver x to earn over driver y on average.

Caution

The plot below isn’t symmetric over the right diagonal - we are strictly comparing the driver on the X axis to the driver on the Y axis.

def make_comparison(idata, idx, groups, size=1000):
    columns = {}
    for idx_a, name_a in enumerate(groups):
        for idx_b, name_b in enumerate(groups):
            pp_a = idata.posterior_predictive["y"][:, :, idx == idx_a].values.flatten()
            pp_b = idata.posterior_predictive["y"][:, :, idx == idx_b].values.flatten()

            samples_a = np.random.choice(pp_a, size=size)
            samples_b = np.random.choice(pp_b, size=size)

            if idx_a != idx_b:
                points_over = (samples_a - samples_b).mean()
            else:
                points_over = 0

            columns.setdefault(name_a, []).append(points_over)

    comparison_df = pd.DataFrame.from_dict(columns).set_index(groups)
    mask = np.triu(np.ones_like(comparison_df, dtype=bool))

    return comparison_df, mask
comparison_df, mask = make_comparison(zi_unpooled_idata, idx, labels)
Code 
sns.set_theme(style="white")

cmap = sns.diverging_palette(230, 20, as_cmap=True)

f, ax = plt.subplots(figsize=(11, 9))

ax = sns.heatmap(
    comparison_df,
    cmap=cmap,
    mask=mask,
    annot=True,
    center=0,
    square=True,
    linewidths=0.5,
    cbar_kws={"shrink": 0.5},
    annot_kws={"fontsize": 8},
).set(title="Driver points expected over rival");
Figure 24: Expected points earned by driver x over driver y using the zero-inflated model

7 Constructor estimates

We’ll run the same loop for the constructor comparison - first we define a slightly modified zero inflated model, then we sample, validate convergence, and finally use the posterior and posterior predictive to evaluate constructor peformance.

Data preparation is identical - we factorize the constructors and take the points

const_idx, const_labels = pd.factorize(const_data_df["constructor"], sort=True)
const_points = const_data_df["constructor_points"]

We adjust the priors slightly, to account for differences in the constructors scoring system:

mu_const_dist = pz.Normal()
pz.maxent(mu_const_dist, np.log(5), np.log(30), 0.9);
Figure 25: Prior for the μ parameter for fitting the zero inflated model to the constructor data 
alpha_const_dist = pz.Gamma()
pz.maxent(alpha_const_dist, 1, 10, .9);
Figure 26: Prior for the α parameter for fitting the zero inflated model to the constructor data 
psi_const_dist = pz.Beta()
pz.maxent(psi_const_dist, .9, .99, .9);
Figure 27: Prior for the ψ parameter for fitting the zero inflated model to the constructor data 
with pm.Model(
    coords={"constructor": const_labels, "idx": const_idx}
) as const_zi_unpooled_model:
    μ = pm.Normal("μ", mu_const_dist.mu, mu_const_dist.sigma, dims="constructor")
    μ_ = pm.Deterministic("μ_", pm.math.exp(μ), dims="constructor")

    α = pm.Gamma("α", alpha_const_dist.alpha, alpha_const_dist.beta, dims="constructor")

    ψ = pm.Beta("ψ", psi_const_dist.alpha, psi_const_dist.beta, dims="constructor")

    y = pm.ZeroInflatedNegativeBinomial(
        "y",
        psi=ψ[const_idx],
        alpha=α[const_idx],
        mu=μ_[const_idx],
        observed=const_points,
        dims="idx",
    )
with const_zi_unpooled_model:
    const_prior_pred = pm.sample_prior_predictive(samples=1000)
Sampling: [y, α, μ, ψ]
az.plot_ppc(const_prior_pred, group="prior", figsize=(12, 6));
Figure 28: Prior predictive distribution for the zero-inflated model when fitted to the constructors data 
with const_zi_unpooled_model:
    const_idata = pm.sample(target_accept=0.9, idata_kwargs={"log_likelihood": True})
    pm.sample_posterior_predictive(const_idata, extend_inferencedata=True)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [μ, α, ψ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 6 seconds.
Sampling: [y]
100.00% [8000/8000 00:05<00:00 Sampling 4 chains, 0 divergences]
100.00% [4000/4000 00:03<00:00] 
az.plot_trace(const_idata, var_names=["μ"], compact=False);
Figure 29: Traceplots of the μ parameter for the zero-inflated model when fitted to the constructors data 
plot_posterior_predictive_checks(const_idata);
Figure 30: Posterior predictive checks, p/u-value, and LOO for the zero-inflated model when fitted to the constructors data 
az.loo(const_idata)
Computed from 4000 posterior samples and 140 observations log-likelihood matrix.

         Estimate       SE
elpd_loo  -472.93     9.48
p_loo       12.07        -
------

Pareto k diagnostic values:
                         Count   Pct.
(-Inf, 0.5]   (good)      139   99.3%
 (0.5, 0.7]   (ok)          1    0.7%
   (0.7, 1]   (bad)         0    0.0%
   (1, Inf)   (very bad)    0    0.0%
az.plot_forest(const_idata, var_names=["μ_"], combined=True, figsize=(12, 6));
Figure 31: Forest of the posterior distribution of the μ parameter for the zero-inflated model when fitted to the constructors data
Code 
sns.set_theme(style="white")

cmap = sns.diverging_palette(230, 20, as_cmap=True)

f, ax = plt.subplots(figsize=(11, 9))

comparison_df, mask = make_comparison(const_idata, const_idx, const_labels)

ax = sns.heatmap(
    comparison_df,
    cmap=cmap,
    mask=mask,
    annot=True,
    center=0,
    square=True,
    linewidths=0.5,
    cbar_kws={"shrink": 0.5},
    annot_kws={"fontsize": 8},
).set(title="Constructor points expected over rival");
Figure 32: Expected points earned by constructor x over constructor y using the zero-inflated model

8 Conclusion

None of the results here are that surprising, but it’s nonetheless useful to confirm our intuition for who’s a good pick and who isn’t. That said, the estimates should be taken with more than a grain of salt - the model we used is quite rudimentary (for one, it doesn’t account for performance trends as the season progresses), and modeling the summed fantasy points directly leads to a lot of detail getting obscured and left out.

%load_ext watermark
%watermark -n -u -v -iv
The watermark extension is already loaded. To reload it, use:
  %reload_ext watermark
Last updated: Tue Sep 05 2023

Python implementation: CPython
Python version       : 3.11.4
IPython version      : 8.14.0

numpy     : 1.25.2
tqdm      : 4.66.1
json      : 2.0.9
preliz    : 0.3.2
scipy     : 1.10.1
arviz     : 0.16.1
matplotlib: 3.7.2
pymc      : 5.7.2
pandas    : 2.1.0
sys       : 3.11.4 (main, Jun 28 2023, 19:51:46) [GCC]
requests  : 2.31.0
seaborn   : 0.12.2

Footnotes

  1. see the intro to this for more details: https://www.pymc.io/projects/examples/en/latest/generalized_linear_models/GLM-negative-binomial-regression.html↩︎

  2. see this for a quick summary of model checking techniques: https://www.pymc.io/projects/docs/en/stable/learn/core_notebooks/pymc_overview.html#model-checking↩︎

  3. see: https://bayesiancomputationbook.com/markdown/chp_02.html#effective-sample-size↩︎

  4. see: https://bayesiancomputationbook.com/markdown/chp_02.html#potential-scale-reduction-factor-hat-r↩︎

  5. see: https://bayesiancomputationbook.com/markdown/chp_02.html#monte-carlo-standard-error↩︎

  6. see: https://bayesiancomputationbook.com/markdown/chp_02.html#understanding-your-predictions↩︎

  7. see: https://bayesiancomputationbook.com/markdown/chp_02.html#fig-posterior-predictive-check-pu-values↩︎

  8. see: https://oriolabrilpla.cat/en/blog/posts/2019/loo-pit-tutorial.html↩︎

  9. for a detailed guide on interpreting the bpv plots see: https://bayesiancomputationbook.com/markdown/chp_02.html#fig-posterior-predictive-many-examples↩︎

  10. see: https://sjster.github.io/introduction_to_computational_statistics/docs/Production/PyMC3.html#hdi↩︎

  11. see: https://bayesiancomputationbook.com/markdown/chp_02.html#cross-validation-and-loo↩︎

  12. see: https://bayesiancomputationbook.com/markdown/chp_02.html#model-comparison↩︎

  13. for much more information on cross validation see: https://avehtari.github.io/modelselection/CV-FAQ.html#12_What_is_the_interpretation_of_ELPD__elpd_loo__elpd_diff↩︎